Question

A box with a volume of 5 m3 is to be constructed with a gold-plated top, silver-plated bottom, and copper-plated sides. If gold plate costs $110 per square meter, silver plate costs $30 per square meter, and copper plate costs $14 per square meter, find the dimensions that will minimize the cost of the materials for the box.

Answer 1

The dimensions are 1 m × 1 m × 5 m

Step-by-step explanation:

Let the dimension be x, y, z

Volume = xyz = 5 m³ ................(1)

According to question:

Cost function, C = 110(xy) + 30(xy) + 14(2xz+2yz)

or

C = 140xy + 28xz + 28yz ..........(2)

We need to maximise (2)

Given condition (1)

Using the concept of lagranges multipliers

`\\(\partial (xyz))/(\partial x)=\lambda (\partial )/(\partial x)140xy+28xz+28yz`

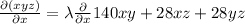
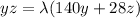`yz=\lambda(140y+28z)` ...........(3)

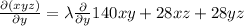
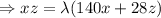`\\(\partial (xyz))/(\partial y)=\lambda (\partial )/(\partial y)140xy+28xz+28yz`

`\Rightarrow xz=\lambda(140x+28z)` ...........(4)

`(\partial (xyz))/(\partial z)=\lambda (\partial )/(\partial z)140xy+28xz+28yz`

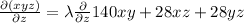
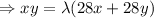`\Rightarrow xy=\lambda(28x+28y)` ...........(5)

From (3) and (4) and(5)

140xy + 28xz = 140xy + 28yz = 28xz + 28yz

thus,

140xy + 28xz = 140xy + 28yz

or

28xz = 28 yz

or

x = y ............(a)

140xy + 28yz = 28xz + 28yz

substituting x from (a)

140(y)y + 28yz = 28(y)z + 28yz

or

140y² = 28yz

or

5y = z

and,

volume = 5 m³

or

xyz = 5 m³

or

x(x)(5y) = 5 m³

or

x²(5x) = 5 m³

or

5x³ = 5 m³

or

x = 1 m

Hence,

y = x = 1 m

and,

z = 5y = 5(1) = 5 m

Therefore,

The dimensions are 1 m × 1 m × 5 m