Answer:
The dimensions are 1 m × 1 m × 5 m
Step-by-step explanation:
Let the dimension be x, y, z
Volume = xyz = 5 m³ ................(1)
According to question:
Cost function, C = 110(xy) + 30(xy) + 14(2xz+2yz)
or
C = 140xy + 28xz + 28yz ..........(2)
We need to maximise (2)
Given condition (1)
Using the concept of lagranges multipliers
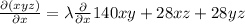
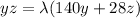 ...........(3)
...........(3)
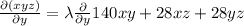
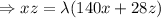 ...........(4)
...........(4)
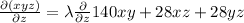
 ...........(5)
...........(5)
From (3) and (4) and(5)
140xy + 28xz = 140xy + 28yz = 28xz + 28yz
thus,
140xy + 28xz = 140xy + 28yz
or
28xz = 28 yz
or
x = y ............(a)
140xy + 28yz = 28xz + 28yz
substituting x from (a)
140(y)y + 28yz = 28(y)z + 28yz
or
140y² = 28yz
or
5y = z
and,
volume = 5 m³
or
xyz = 5 m³
or
x(x)(5y) = 5 m³
or
x²(5x) = 5 m³
or
5x³ = 5 m³
or
x = 1 m
Hence,
y = x = 1 m
and,
z = 5y = 5(1) = 5 m
Therefore,
The dimensions are 1 m × 1 m × 5 m