 form of line passing through (5, –7.5) and line having x y-intercept of 10 is
form of line passing through (5, –7.5) and line having x y-intercept of 10 is
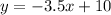
Solution:
Need to find the equation of a line in form of

Given that
Line is passing through point (5, –7.5) and y intercept of line = 10
y intercept is a point where line crosses the y axis.
In our case line have y intercept of 10, which means line crosses y axis at 10. Also at y axis, value of x is always 0.
So we can say that line passes through point (0, 10).
Now we can say that we need equation of line passing through (5, –7.5) and (0, 10).
Equation of line passing through point
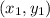 and
and
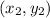 is given by
is given by
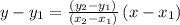
In our case
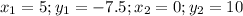
Substituting given value in (1) we get
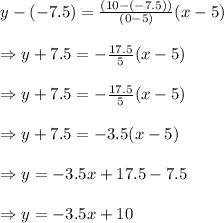
Hence
 form of line passing through (5, –7.5) and line having x y-intercept of 10 is
form of line passing through (5, –7.5) and line having x y-intercept of 10 is
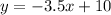 .
.