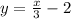Answer:
The equation of the line is
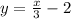
Explanation:
Given
Point 1 (0, -2)
Point 2 (6, 0).
Required
What is the equation of the line?
To get the equation of the line, we have to calculate the two -point form gradient formula.
Let gradient be represented by m
The expression for m is as follows;
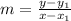 and
and
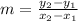
Since m = m, we have

Such that

By Substituting these values in the expression above, we'll get the equation of the line

becomes

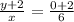
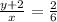
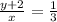
Multiply 3x to both sides
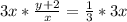

Open bracket
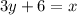
Make y the subject of formula
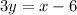
Divide both sides by 3
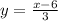

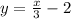
Hence, the equation of the line is