Answer:
Part A:
interval=(3.0452,3.3548,)
Part B:
Interval=(3.0824,3.3176)
Part C:
Interval=(3.100763.29924,)
Part D:
Z=0.833
CI=91%
Explanation:
CI Z
90% 1.645
95% 1.96
99% 2.58
The formula we are going to use is:
Interval=X±
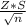
Where
X is the mean value
S is the standard deviation
n is the sample size
Z is the distribution
Part A:
Interval=3.2±
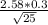
Interval=3.2±0.1548
interval=(3.0452,3.3548)
Part B:
Interval=3.2±
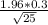
Interval=3.2±0.1116
Interval=(3.0824,3.3176)
Part C:
Interval=3.2±
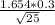
Interval=3.2±0.09924
Interval=(3.10076,3.29924)
Part D:
3.2-3.15=3.25-3.2=0.05
0.05=
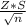
0.05=
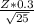
Z=0.833
CI=91%