Answer:
The maximum efficiency possible of such a heat engine is 8.9%.
Step-by-step explanation:
Given that,
High temperature = 30°C
Depth = 1200 m
low temperature = 3°C
We need to calculate the maximum efficiency
Using formula of efficiency
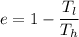
Where,
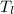 = low temperature
= low temperature
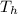 =High temperature
=High temperature
Put the value into the formula
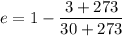
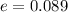
The efficiency in percentage,
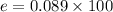
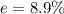
Hence, The maximum efficiency possible of such a heat engine is 8.9%.