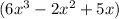Answer:
The Sum of the Expression
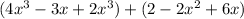 is
is
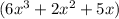
Explanation:
Given :
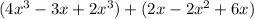
Now we will use the BODMAS method Which has a rule to use it and this rule states that if any equation has bracket, off, Divide ,Multiply , addition and subtraction signs then we will solve first Bracket then Off then Division then Multiplication then Addition and at last subtraction.
So,
Sum=
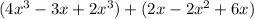
Sum=
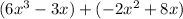
Sum=

Sum=
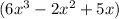
Hence the Sum of the above Expression is