Question

A gasoline tank for a certain car is designed to hold 14.0 gal of gas. Suppose that the variable x = actual capacity of a randomly selected tank has a distribution that is well approximated by a normal curve with mean 14 gal and standard deviation 0.2 gal. (Round all answers to four decimal places.)

(a) What is the probability that a randomly selected tank will hold at most 13.7 gal?

P(x ? 13.7) =

(b) What is the probability that a randomly selected tank will hold between 13.4 and 14.3 gal?

P(13.4 ? x ? 14.3) =

(c) If two such tanks are independently selected, what is the probability that both hold at most 14 gal?

P(x ? 14) =

Answer 1

A gasoline tank for a certain car is designed to hold 14.0 gal of gas.

`\mu = 14`

`\sigma = 0.2`

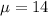
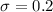
a)What is the probability that a randomly selected tank will hold at most 13.7 gal?

We are supposed to find
`P(x \leq 13.7)`

`z=(x-\mu)/(\sigma)`

`z=(13.7-14)/(0.2)`

`z=-1.5`

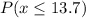
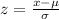
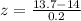
Refer the z table for p value

p value = 0.0668

So,
`P(x \leq 13.7)= 0.0668`

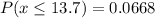
The probability that a randomly selected tank will hold at most 13.7 gal is 0.0668

b)What is the probability that a randomly selected tank will hold between 13.4 and 14.3 gal?

We are supposed to find
`P(13.4<x<14.3)`

`z=(x-\mu)/(\sigma)`

`z=(13.4-14)/(0.2)`

`z=-3`

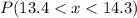
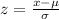
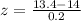
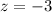
P(x<13.4)=P(z<-3)= 0.0013

`z=(x-\mu)/(\sigma)`

`z=(14.3-14)/(0.2)`

`z=1.5`

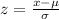
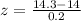
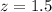
P(x<14.3)= 0.9332

`P(13.4<x<14.3)=P(x<14.3)-P(x<13.4)=0.9332- 0.0013=0.9319`

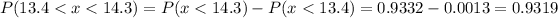
The probability that a randomly selected tank will hold between 13.4 and 14.3 gal is 0.9319

(c) If two such tanks are independently selected, what is the probability that both hold at most 14 gal?

We are supposed to find
`P(x \leq 14)`

`z=(x-\mu)/(\sigma)`

`z=(14-14)/(0.2)`

`z=0`

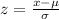
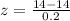
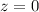
Refer the z table for p value

p value = 0.5

So,
`P(x \leq 14)= 0.5`

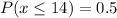
Two such tanks are independently selected, the probability that both hold at most 14 gal = 0.5 * 0.5 = 0.25

Hence If two such tanks are independently selected, the probability that both hold at most 14 gal is 0.25