Question

A function y(t) satisfies the differential equation dy dt = y4 − 9y3 + 20y2. (a) What are the constant solutions of the equation? (b) For what values of y is y increasing? (c) For what values of y is y decreasing?

Answer 1

a) y = 0, y = 4 and y = 5

b) y ⊂ (- ∞, 0) ∪ (0, 4) ∪ (5, ∞)

c) y ⊂ (4,5)

Explanation:

Data provided in the question:

function y(t) satisfies the differential equation:

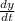`(dy)/(dt)` = y⁴ − 9y³ + 20y²

Now,

a) For constant solution

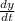`(dy)/(dt)` = 0

or

y⁴ − 9y³ + 20y² = 0

or

y² (y² - 9y + 20 ) = 0

or

y²(y² -4y - 5y + 20) = 0

or

y²( y(y - 4) -5(y - 4)) = 0

or

y²(y - 4)(y - 5) = 0

therefore, solutions are

y = 0, y = 4 and y = 5

b) for y increasing

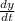`(dy)/(dt)` > 0

or

y²(y - 4)(y - 5) > 0

or

y²

y ⊂ (- ∞, 0) ∪ (0, 4) ∪ (5, ∞)

c) for y decreasing

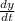`(dy)/(dt)` < 0

or

y²(y - 4)(y - 5) > 0

or

y²

y ⊂ (4,5)