Answer: We reject the null hypothesis, and we use Normal distribution for the test.
Explanation:
Since we have given that
We claim that
Null hypothesis :
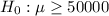
Alternate hypothesis :
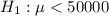
There is 5% level of significance.
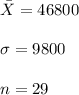
So, the test statistic would be
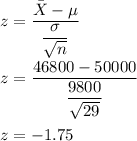
Since alternate hypothesis is left tailed test.
So, p-value = P(z≤-2.31)=0.0401
And the P-value =0.0401 is less than the given level of significance i.e. 5% 0.05.
So, we reject the null hypothesis, and we use Normal distribution for the test.