Question

A researcher is testing the effectiveness of a new herbal supplement that claims to improve physical fitness. A sample of n = 16 college students is obtained and each student takes the supplement daily for six weeks. At the end of the 6-week period, each student is given a standardized fitness test and the average score for the sample is M = 39. For the general population of college students, the distribution of test scores is normal with a mean of µ = 35 and a standard deviation of σ = 12. Do students taking the supplement have significantly better fitness scores? Use a one-tailed test with α = .05.

Answer 1

There is insufficient evidence to support students taking the supplement have significantly better fitness scores

Explanation:

Sample size = n = 16

The average score for the sample is M = 39

µ = 35

σ = 12

We are supposed to find Do students taking the supplement have significantly better fitness scores

Use a one-tailed test with α = .05.

`H_0:\mu = 35\\H_a:\mu>35`

`z=(x-\mu)/((\sigma)/(√(n)))`

`z=(39-35)/((12)/(√(16)))`

`z=1.33`

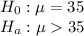
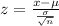
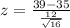
Refer the z table for p value

P(z>1.33)=1-P(z<1.33)=1-0.908=0.092

α = .05

p value > α

So, we failed to reject null hypothesis.

So, there is insufficient evidence to support students taking the supplement have significantly better fitness scores