Question

A small manufacturer constructs refrigerators. The fixed monthly cost is $200,000, and it costs $450 to produce one refrigerator. The average cost function to produce X refrigerators is represented by: c(x)= 200,000+450x/x. What is the horizontal asymptote of C(x)?

Answer 1

y=450

Explanation:

It is given that the fixed monthly cost is $200,000, and it costs $450 to produce one refrigerator.

Total cost of x refrigerator is

`T(x)=200,000+450x`

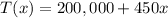
The average cost function to produce X refrigerators is represented by:

`C(x)=(200,000+450x)/(x)`

If the degree of numerator and denominator are same, then horizontal asymptote is

`y=(p)/(q)`

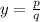
where, p is the leading coefficient of numerator and q is leading coefficient of denominator.

In the above function leading coefficient of numerator is 450 and leading coefficient of denominator is 1. So, horizontal asymptote is

`y=(450)/(1)`

`y=450`

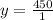
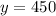
Therefore, the horizontal asymptote of C(x) is y=450.

Answer 2

Answer: Horizontal asymptote of c(x) is 450.

Explanation:

Since we have given that

Cost to produce one refrigerator = $450

Fixed monthly cost = $200,000

So, Average cost function to produce x refrigerators is given by

`c(x)=(200000+450x)/(x)`

Horizontal asymptote of c(x) would be

`(450x)/(x)\\\\=450`

Hence, Horizontal asymptote of c(x) is 450.