Question

A student desired to invest $1,540 into an investment at 9% compounded semiannually for 6 years. With all else equal, what is the future value of this initial investment after the six year period

Answer 1

The future value of this initial investment after the six year period is $2611.6552

Explanation:

Consider the provided information.

A student desired to invest $1,540 into an investment at 9% compounded semiannually for 6 years.

Future value of an investment:
`FV=P(1+r)^n`

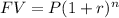
Where Fv is the future value, p is the present value, r is the rate and n is the number of compounding periods.

9% compounded semiannually for 6 years.

Therefore, the value of r is:
`r=(0.09)/(2)=0.045`

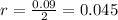
Number of periods are: 2 × 6 = 12

Now substitute the respective values in the above formula.

`FV=1540(1+0.045)^(12)`

`FV=1540(1.045)^(12)`

`FV=1540(1.69588)`

`FV=2611.6552`

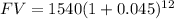
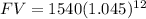
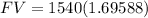
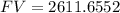
Hence, the future value of this initial investment after the six year period is $2611.6552