Question

Consider an LC circuit in which L = 490 mH and C = 0.116 �F.

(a) What is the resonance frequency ?0?
krad/s

(b) If a resistance of 1.02 k? is introduced into this circuit, what is the frequency of the damped oscillations?


(c) By what percentage does the frequency of the damped oscillations differ from the resonance frequency?

Answer 1

(a) 4190 rad/sec

(b) 4064 rad/sec

(c) Percentage change is 3 %

Step-by-step explanation:

We have given inductance
`L=490mH=490* 10^(-3)H`

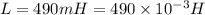
Capacitance
`C=0.116\mu F=0.116* 10^(-6)F`

We know that resonance frequency is given by
`\omega =(1)/(√(LC))=\frac{1}{\sqrt{490* 10^(-3)* 0.116* 10^(-6)}}=4190rad/sec`

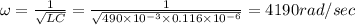
Now resistance is given as R = 1020 ohm '

(b) We know that damped frequency is given by

`\omega =\sqrt{(1)/(LC)-((R)/(2L))^2}=\sqrt{(1)/(490* 10^(-3)* 0.116* 10^(-3))-((1020)/(2* 490* 10^(-3)))^2}=4064rad/sec`

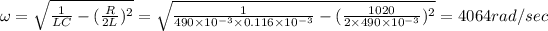
(c) Percentage change in frequency
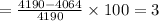`=(4190-4064)/(4190)* 100=3`%