Question

A theme park charges a flat fee of $500 for group bookings of more than 25 tickets, plus $20 per ticket for up to 100 tickets and $17 per ticket thereafter. If x represents the number of tickets sold under the group booking option, complete the limit equation that represents the average cost per ticket as the number of tickets purchased becomes very high.

Answer 1

Answer:
`\lim_(n \to \infty) a_n (2500+17(x-100))/(x) =17`

Step-by-step explanation: I got this correct on Edmentum.

Answer 2

The required equation is:
`\lim_(x \to \infty) (2500+17(x-100))/(x)=17`

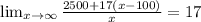
Explanation:

Consider the provided information.

Let x represents tickets sold.

A theme park charges a flat fee of $500 for group bookings of more than 25 tickets, plus $20 per ticket for up to 100 tickets and $17 per ticket thereafter.

The charges for booking 100 tickets will be:

`500 + 20* 100 = \$2500`

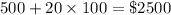
If you by more than 100 tickets theme park charges $17,

Thus, charges for x tickets will be =
`2500+ 17(x - 100)`

The limit equation represents the average cost per ticket as the number of tickets purchased becomes very high.

The Cost of one ticket of the theme park =
`\lim_(x \to \infty) (2500+17(x-100))/(x)`

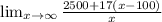
Now solve the above limit equation that will gives you the average cost per ticket as the number of tickets purchased becomes very high.

`\lim_(x \to \infty) (2500+17(x-100))/(x)= \lim_(x \to \infty)(2500)/(x)+17-(1700)/(x)`

`\lim_(x \to \infty)(2500)/(x)+17-(1700)/(x)=0+17-0`

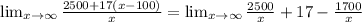
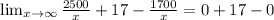
Hence, the cost per ticket is $17 as the number of tickets purchased becomes very high.