Question

A wall clock is equally divided into 12 sections. If the clock reads 8:00 and has a diameter of 12.5 inches, find the area of the smaller sector formed by the minute and hour hands.

Answer 1

The area of the sector is 81.8 square inches.

Explanation:

The wall clock has handas that move 360°. So, if it's equally distributed then, we can divide

`(360\°)/(12)= 30\°`

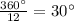
Thich means that during each interval of hour, the hands move 30°.

So, if the wall clock is showing 8 o'clock, than one hand is pointing 12, which is gonna be the reference point 0°. The hour hand would be at number 8, which forms an angle of

`8(30\°)=240 \°`

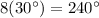
Now, to find the circular sector area we used the following formula

`A= (\theta)/(360 \°) * \pi r^(2)`

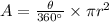
Where
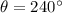`\theta = 240 \°` and
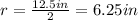`r=(12.5 in)/(2)= 6.25 in`, because the radius is defined as half the diameter.

Replacing all these values and
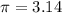`\pi =3.14`, we have

`A= (240\°)/(360 \°) * (3.14) (6.25in)^(2)=81.8 in^(2)`

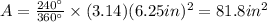
Therefore, the area of the smaller sector formed by the minute and hour hands is 81.8 square inches.

Answer 2

Answer: Our required area would be 11.93 sq. inches.

Explanation:

Since we have given that

Number of sections = 12

Angle formed in every 5 minutes is given by

`(360)/(12)=30^\circ`

Diameter = 12.5 inches

Radius =
`(12.5)/(2)=6.25\ inches`

Area of the smaller sector formed by the minute and hour hands would be

`(\theta)/(360^\cir)* \pi r^2\\\\=(30)/(360)* (22)/(7)* 6.75* 6.75\\\\=11.93\ sq.\ inches`

Hence, our required area would be 11.93 sq. inches.