Question

Coherent light with wavelength 610 nm passes through two very narrow slits, and theinterference pattern is observed on a screen a distance of 3.00{\rm m} from the slits. The first-order bright fringe is adistance of 4.84 {\rm mm} from the center of the central bright fringe.For what wavelength of light will thefirst-order dark fringe be observed at this same point on thescreen?Express your answer in micrometers(not in nanometers).

Answer 1

= 1220 nm

= 1.22 μm

Step-by-step explanation:

given data:

wavelength
`\lambda = 610 nm = 610*  10 ^(-9) m`

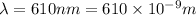
distance of screen from slits D = 3 m

1st order bright fringe is 4.84 mm

condition for 1 st bright is

`d sin \theta =\lambda` ---( 1)

and
`tan \theta = (y)/( D)`

`\theta = tan^(-1)((y )/(D))`

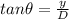
= 0.0924 degrees

plug theta value in equation 1 we get

`d sin ( 0.0924) = 610 * 10 ^(-9)`

`d = 3.78* 10^(-4) m`

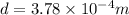
condition for 1 st dark fringe

`<strong> d sin \theta =(λ')/(2)</strong>`

`\lambda '= 2 d sin\theta`

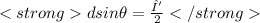
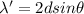
= 2λ since from eq (1)

= 1220 nm

= 1.22 μm