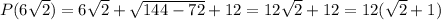Question

Among all right triangles whose hypotenuse has a length of 12 cm, what is the largest possible perimeter?

Answer 1

Largest perimeter of the triangle =

`P(6√(2)) = 6√(2) + √(144-72) + 12 = 12√(2) + 12 = 12(\sqrt2 + 1)`

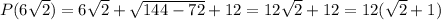
Explanation:

We are given the following information in the question:

Right triangles whose hypotenuse has a length of 12 cm.

Let x and y be the other two sides of the triangle.

Then, by Pythagoras theorem:

`x^2 + y^2 = (12)^2 = 144\\y^2 = 144-x^2\\y = √(144-x^2)`

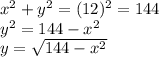
Perimeter of Triangle = Side 1 + Side 2 + Hypotenuse.

`P(x) = x + √(144-x^2) + 12`

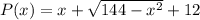
where P(x) is a function of the perimeter of the triangle.

First, we differentiate P(x) with respect to x, to get,

`(d(P(x)))/(dx) = (d(x + √(144-x^2) + 12))/(dx) = 1-\displaystyle(x)/(√(144-x^2))`

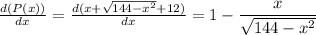
Equating the first derivative to zero, we get,

`(dP(x)))/(dx) = 0\\\\1-\displaystyle(x)/(√(144-x^2)) = 0`

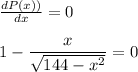
Solving, we get,

`1-\displaystyle(x)/(√(144-x^2)) = 0\\\\x = √(144-x^2)}\\\\x^2 = 144-x^2\\\\x = √(72) = 6√(2)`

Again differentiation P(x), with respect to x, using the quotient rule of differentiation.

`(d^2(P(x)))/(dx^2) = \displaystyle\frac{-(144-x^2)^{(3)/(2)}-x^2}{(144-x)^{(3)/(2)}}`

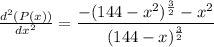
At x =
`6√(2)`,

`(d^2(V(x)))/(dx^2) < 0`

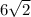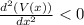
Then, by double derivative test, the maxima occurs at x =
`6√(2)`

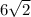
Thus, maxima occurs at x =
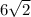`6√(2)` for P(x).

Thus, largest perimeter of the triangle =

`P(6√(2)) = 6√(2) + √(144-72) + 12 = 12√(2) + 12 = 12(\sqrt2 + 1)`