Question

A bus contains a 1500 kg, 0.600 m radius flywheel (a disk) and has a total mass of 10,000 kg.

(a) Calculate the angular velocity the flywheel must have, in rad/s, to contain enough energy to take the bus from rest to a speed of 24.5 m/s, assuming 85.0% of the rotational kinetic energy can be transformed into translational energy
(b) How high a hill, in meters, can the bus climb with this stored energy and still have a speed of 5.00 m/s at the top of the hill?

Answer 1

Step-by-step explanation:

Given that,

Mass of the bus, m = 1500 kg

Mass of the flywheel, M = 10,000 kg

Radius of flywheel, r = 0.6 m

Speed of the bus, v = 24.5 m/s

(a) Let
`\omega` is the angular velocity of the flywheel. It is assumed that 85.0% of the rotational kinetic energy can be transformed into translational energy. Using the conservation of energy as :

`85\%\ of\ K_r=K_t`

`0.85* (1)/(2)I\omega^2=(1)/(2)Mv^2`

`0.85* I\omega^2=Mv^2`

`0.85* (1)/(2)mr^2\omega^2=Mv^2`

`\omega^2=(Mv^2)/(0.85* mr^2)`

`\omega^2=(10000 * (24.5)^2)/(0.85* 1500* (0.6)^2)`

`\omega=114.35\ rad/s`

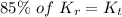
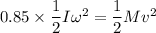
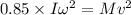
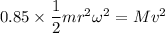
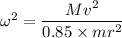
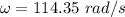
(b) Let h is the height climb with this stored energy. Again using the conservation of energy as :

`0.85K_r=K_t+mgh`

`0.85* (1)/(2)I\omega^2=(1)/(2)Mv^2+Mgh`

`Mgh=0.85* (1)/(4)mr^2\omega^2-(1)/(2)Mv^2`

`h=(0.85* (1)/(4)mr^2\omega^2-(1)/(2)Mv^2)/(Mg)`

`h=(0.85* (1)/(4)1500* (0.6)^2* (114.35)^2-(1)/(2)* 10000* 24.5^2)/(10000* 9.8)`

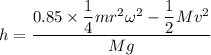
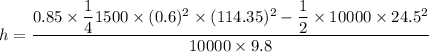
h = 15.31 meters

Hence, this is the required solution.