Question

Enter T or F depending on whether the statement is true or not. (You must enter T or F -- True and False will not work.) If it is true do a proof and if it is false provide a counter-example (Of course the proofs and counter-examples must be written down on paper!). If a is divisible by 3 then a is divisible by 9. The substraction of 2 rational numbers is rational. A sufficient condition for an integer to be divisible by 8 is that it is divisible by 2. A sufficient condition for an integer to be divisible by 6 is that it is divisible by 2. If a is divisible by 9 then a is divisible by 3. The product of 2 consecutives integers is even. Answer the following questions. 30 division 3 = , 30 mod 3 = -26 division 5 = , - 26 mod 5 = 28 division 4 = , 28 mod 4 = -29 division 10 = , -29 mod 10 = 24 division 9 = , 24 mod 9 = -28 division 6 = , -28 mod 6 = 965255471 mod 101 = 630153353 mod 101 =

Answer 1

See below

Explanation:

If a is divisible by 3 then a is divisible by 9

FALSE

Counter-example

6 is divisible by 3 but not by 9

The subtraction of 2 rational numbers is rational.

TRUE

Proof

If a, b are two rational numbers

`\large a=(p)/(q)\;b=(r)/(s)`

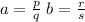
for some integers p, q, r, s.

Then

`\large a-b=(p)/(q)-(r)/(s)=(ps-qr)/(qs)`

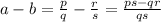
since ps-qr and qs are integers, a-b is rational

A sufficient condition for an integer to be divisible by 8 is that it is divisible by 2

FALSE

Counter-example

4 is divisible by 2 but not by 8

A sufficient condition for an integer to be divisible by 6 is that it is divisible by 2

FALSE

Counter-example

4 is divisible by 2 but not by 6

If a is divisible by 9 then a is divisible by 3.

TRUE

Proof

If a is divisible by 9, then a = 9k for some integer k, but 9=3*3, so a = 3*(3k).

Since 3k is integer, a is divisible also by 3.

The product of 2 consecutive integers is even.

TRUE

Proof

Let p, q be two consecutive integers, then either p is even or odd.

Suppose first p is even. Then

p = 2n and q = 2n+1, so p*q=2n(2n+1)=2n*2n+2n=2(n*2n+n)

since (n*2n+n) is integer p*q is even.

Suppose now p is odd

p = 2n+1 q = 2n+2, then

p*q=(2n+1)(2n+2)=2n*2n+2*2n+2n+2=2(n*2n+2n+n+1)

since (n*2n+2n+n+1) is integer p*q is also even.

Answer the following questions:

30 division 3 =

10

30 mod 3 =

0 (the remainder when dividing 30 by 3)

-26 division 5 =

-5 (plus remainder -1)

-26 mod 5 =

-1 (the remainder when dividing -26 by 5)

28 division 4 =

7

28 mod 4 =

0

-29 division 10 =

-2 (plus remainder -9)

-29 mod 10 =

-9

24 division 9 =

2 (plus remainder 6)

24 mod 9 =

6

-28 division 6=

-4 (plus remainder -4)

-28 mod 6 =

-4

965255471 mod 101 =

87 (the remainder when dividing 965255471 by 101)

630153353 mod 101 =

11 (the remainder when dividing 630153353 by 101)