Question

The endpoints of RS are R(–5, 12) and S(4, –6). What are the coordinates of point T, which divides RS into a 4:5 ratio?

Answer 1

The coordinates of T are (-1,4)

Explanation:

The given coordinates of R and S are R(-5,12) and S(4, -6).

The point T divides RS in the ratio 4 : 5.

Let the coordinates of T = (x,y)

Now, by SECTION FORMULA:

If, m1 : m2 is the given ratio, then

`(x,y)  = ((m_1x_2 + m_2x_1)/(m_1+m_2) ,(m_1y_2 + m_2y_1)/(m_1+m_2))`

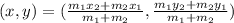
So, here:
`(x,y)  = ((4(4) + 5(-5))/(4+5) ,(4(-6) + 5(12))/(4+5))`

or,
`(x,y)  = ((16 -25)/(9) ,(-24+60)/(9) )  \implies (x,y)  = ((-9)/(9) (36)/(9) )`

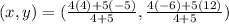
or, (x, y) = (-1,4)

Hence, the coordinates of T are (-1,4)