Question

It costs more to produce defective items - since they must be scrapped or reworked - than it does to produce non-defective items. This simple fact suggests that manufacturers should ensure the quality of their products by perfecting their production processes instead of depending on inspection of finished products (Deming, 1986). In order to better understand a particular metal stamping process, a manufacturer wishes to estimate the mean length of items produced by the process during the past 24 hours. (Give answer to nearest whole number.)

a) How many parts should be sampled in order to estimate the population mean to within .1 millimeter (mm) with 90% confidence? Previous studies of this machine have indicated that the standard deviation of lengths produced by the stamping operation is about 2mm. 1083 Correct: Your answer is
b) Time permits the use of a sample size no larger than 100. If a 90% confidence interval for the mean is constructed with n = 100, will it be wider or narrower than would have been obtained using the sample size determined in part a? cannot be determined narrower wider unchanged.

Answer 1

Answer: a) 1082, b) wider.

Explanation:

Since we have given that

Margin of error = 0.1 millimeter = E

Standard deviation = 2 mm = σ

Critical value would be

`z_{(\alpha)/(2)}=z_(0.05)=1.645`

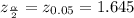
a) Sample size would be

`n=(\frac{z_{(\alpha )/(2)}* \sigma}{E})^2\\\\n=((1.645* 2)/(1))^2\\\\n=1082.41\\\\n=1082`

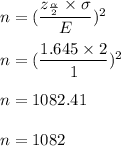
b) Sample size, n = 100

So, the margin of error would be

`E=z_{(\alpha )/(2)}* (\sigma)/(√(n))\\\\E=1.645* (2)/(√(100))\\\\E=1.645* (2)/(10)\\\\E=0.329`

Since the margin of error in b part is more than a part, as we know that the higher the margin of error, the wider the confidence interval.

So, it would have wider confidence interval.

Hence, a) 1082, b) wider.