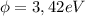Answer:
Knowing that the stopping potential is 1.00 V when the wavelength of the incident light is 296 nm and 2.9 V when the wavelength is 207 nm Planck's constant (h) and the work function (
 ) of the metal are
) of the metal are
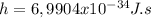 and
and
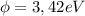 .
.
Step-by-step explanation:
If an electron of a metal surface absorbs the energy of a photon and gets more energy than the binding energy of the metal (given by the work function) then is ejected.
The next equation describes the maximum kinetic energy of the ejected electrons:
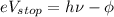
where
 is the charge of the electron
is the charge of the electron
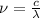 is the frequency of the incident light
is the frequency of the incident light
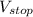 is the stopping potential
is the stopping potential
to determine Planck's constant (
 ) and the work function (
) and the work function (
 ) given the stopping potentials measured at two different wavelengths we have two equations:
) given the stopping potentials measured at two different wavelengths we have two equations:
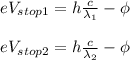
Planck's constant (
 )
)
We use that the speed of light is
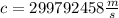 and that
and that

and we replace these values in the equations to get
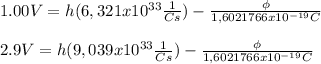
if we substract the second equation with the first one we get that:
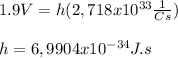
We need to note that this number for Planck's constant is a little over the exact value
 .
.
Work function (
 )
)
Then replacing the value we found for
 in one of the equations relating the stopping potential with the wavelength we get:
in one of the equations relating the stopping potential with the wavelength we get:

we need to make a little change of units to match the two terms in the right side of the equation, so we use

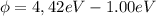
we finally get for the work function