Answer: 34%
Explanation:
According to the Empirical rule,
About 68% of the population lies with in one standard deviation from the mean.
i.e. About 34% of the population lies above one standard deviation from the mean .
and About 34% of the population lies below one standard deviation from the mean.
Given : The distribution of the number of daily requests is bell-shaped ( i.e. Normally distribution) and has a mean of 60 and a standard deviation of 11.
i.e.
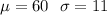
Using the Empirical Rule rule, 34% of the population of lightbulb replacement requests lies above one standard deviation from the mean .
i.e. About 34% of the population of lightbulb replacement requests lies between
 and
and
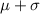
i.e. About 34% of the population of lightbulb replacement requests lies between
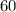 and
and
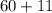
i.e. About 34% of the population of lightbulb replacement requests lies between 60 and 71
Hence, the approximate percentage of lightbulb replacement requests numbering between 60 and 71 = 34%