Answer:
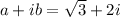 and
and
 .
.
Step-by-step explanation:
Rational number: If a number is defined in the form of p/q, where p and q are integers and q≠0, then it is called a rational number.
For example: 2, 0.2, 3/4 etc.
Irrational number: If a number can not be defined in the form of p/q, where p and q are integers and q≠0, then it is called an irrational number.
For example: √2, 3.222.., π etc.
We need to find two complex numbers, (a+bi) and (c+di), where a and d are irrational numbers and b and c are rational number.
We can choose any irrational numbers for a and d.
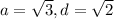
We can choose any rational numbers for b and c.
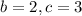
Two complex numbers are
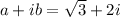

Therefore, the two complex numbers are
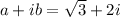 and
and
 .
.