Question

Coyotes are one of the few species of North American animals with an expanding range. The future population of coyotes in a region of Mississippi can be modeled by the equation P = 57+ 10 n(11t + 1), where t is time in years. Use the equation to determine when the population will reach 150? (Round to the nearest tenth of a year.)

Answer 1

Answer: It takes approximately 994.3 years to reach 150.

Explanation:

Since we have given that

Future population of coyotes in a region of Mississippi can be modeled by the equation would be

`P=57+10\ln(11t+1)`

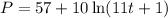
Here, P is the population and t is time in years.

We need to find the time when the population will reach 150.

So, it becomes,

`150=57+10\ln(11t+1)\\\\150-57=10ln(11t+1)\\\\93=10\ln(11t+1)\\\\(93)/(10)=\ln(11t+1)\\\\9.3=\ln(11t+1)\\\\e^(9.3)=11t+1\\\\10938=11t+1\\\\10938-1=11t\\\\10937=11t\\\\t=(10937)/(11)\\\\t=994.3`

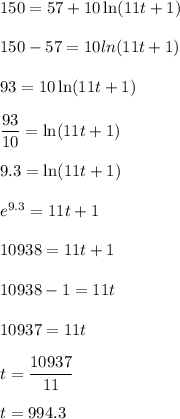
Hence, it takes approximately 994.3 years to reach 150.