The river level raises by 49152 inches in 15 days.
Solution:
The river rose three inches the first day, and each day twice as much as the previous day.
We have to find how much did the river rise in fifteen days
Now, let the normal level be "n", then, first day level will be n + 3 inches
So 1st day raise will be 3
And second day raise will be 2(3)
Now, 3rd day raise will be
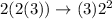
So, this forms geometric progression
A geometric sequence is a sequence with the ratio between two consecutive terms is constant
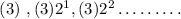
with first term a = 3 and common ratio "r" = 2
Now, we have to find raise after 15 days
The nth term of G.P is given as:
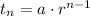
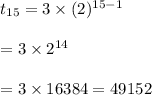
Hence, the river level raise by 49152 inches in 15 days.