Question

The leg of an isosceles triangle is 16 and the measure of one of the angles is 150. Find the area of the triangle.

Answer 1

64

Explanation:

This is very late, but I'm also surprised the other person was off by 0.02, how sad

Answer 2

Area of isosceles triangle is 63.98 square units.

Solution:

Note: Refer the image attached below

Given that leg of an isosceles triangle is 16; Measured of one of the angle is 150; Need to determine area of triangle.

Consider the figure ABC is required isosceles triangle

From given information,

AC = CB = 16 and
`\angle \mathrm{ACB}=150^(\circ)`

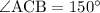
So we have two sides and angle between them. Let us use law of cosine

On applying law of cosine on triangle ABC we get,

`\begin{array}{l}{\mathrm{AB}^(2)=\mathrm{AC}^(2)+\mathrm{CB}^(2)-2 * \mathrm{AC} * \mathrm{CB} \cos \mathrm{C}} \\\\ {=>\mathrm{AB}^(2)=16^(2)+16^(2)-2 * 16 * 16 \cos 150} \\\\ {\Rightarrow \mathrm{AB}^(2)=16^(2)+16^(2)+443.4} \\\\ {\Rightarrow \mathrm{AB}^(2)=955.4} \\\\ {\Rightarrow \mathrm{AB}=30.91}\end{array}`

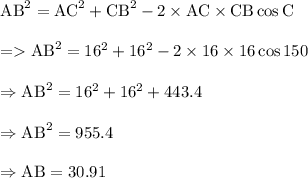
Now we are having three sides of triangle,

AB = 30.91; BC = 16 and CA = 16

As three sides are given, we can apply heron’s formula to determine area of triangle ABC. According to herons formula,

`\begin{array}{l}{\text { Area of Triangle }=√(s(s-a)(s-b)(s-c))} \\\\ {\text { Where } s=(a+b+c)/(2)}\end{array}`

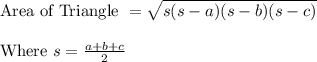
In our case a = AB = 30.91; b = BC = 16; c = CA = 16

`\begin{array}{l}{\text { So } s=(A B+B C+C A)/(2)=(30.91+16+16)/(2)=31.455} \\\\ {\text { Area of Triangle } A B C=√(31.455(31.455-30.91)(31.455-16)(31.455-16))} \\\\ {\Rightarrow \text { Area of Triangle } A B C=√(31.455 * 0.545 * 15.455 * 15.455)=√(4094.72)=63.98}\end{array}`