Question

6(x-k)=5x+4

Show that x must be an even number.

Answer 1

See Below

Explanation:

We will use distributive property [a(b+c) = ab + ac] to simplify the left-hand side of the equation and add like terms and solve for x first. Process shown below:

`6(x-k)=5x+4\\6x-6k=5x+4\\6x-5x=6k+4\\x=6k+4`

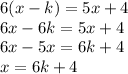
To show x is ALWAYS AN EVEN number, we can plug in a value for k (even and odd) to show that x becomes always even.

Even Number Case:

k = 2 (2 is an even number, any even would be the same):

`x=6k+4\\x=6(2) + 4\\x = 12 + 4\\x = 16`

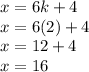
x is 16, which is even number

Odd Number Case:

k = 3 (3 is an odd number, any odd would be the same):

`x=6k+4\\x=6(3) + 4\\x = 18 + 4\\x = 22`

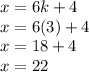
x is 22, which is an even number.

Hence, x will always be an even number (shown).