Answer:
Part a)
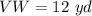
Part b)

Explanation:
The complete question in the attached figure
we know that
The Triangle Mid-segment Theorem states that:The segment joining the midpoints of two sides of a triangle is parallel to the third side, and its length is half the length of that side
step 1
Find out the length of the pathway VW
 -----> by Triangle Mid-segment Theorem
-----> by Triangle Mid-segment Theorem
Because V is the midpoint of XY and W is the midpoint of YZ
so
VW is parallel to XW
we have
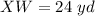
substitute

step 2
Find the length YZ
Applying the Pythagoras Theorem
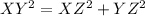
we have
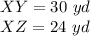
substitute
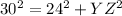
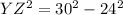
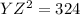
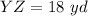
step 3
Find out the length of the pathway VT
 -----> by Triangle Mid-segment Theorem
-----> by Triangle Mid-segment Theorem
Because V is the midpoint of XY and T is the midpoint of XZ
so
VT is parallel to YZ
we have
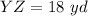
substitute
