Question

Find the circumcenter of the triangle ABC A(-8,5) B(-6,7) C(-8,7)

Answer 1

(-7,6)

Explanation:

The vertices of a triangle ABC are A(-8,5) B(-6,7) C(-8,7).

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

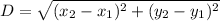
Using distance formula we get

`a=BC=√(\left(-8-\left(-6\right)\right)^2+\left(7-7\right)^2)=2`

`b=AC=√(\left(-8-\left(-8\right)\right)^2+\left(7-5\right)^2)=2`

`c=AB=√(\left(-6-\left(-8\right)\right)^2+\left(7-5\right)^2)=2√(2)`

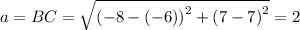
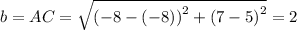
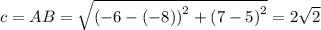
Using these sides, we get

`AB^2=(2√(2))^2=8`

`BC^2+AC^2=2^2+2^2=8`

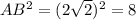
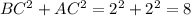
Since
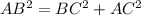`AB^2=BC^2+AC^2`, therefore triangle ABC is a right angled triangle.

Circumcenter of a right angled triangle is the midpoint of hypotenuse.

In triangle ABC, side AB is hypotenuse. So, circumcenter of the triangle ABC is the midpoint of AB.

`Circumcenter=((x_1+x_2)/(2), (y_1+y_2)/(2))`

`Circumcenter=((-8-6)/(2), (5+7)/(2))`

`Circumcenter=((-14)/(2), (12)/(2))`

`Circumcenter=(-7,6)`

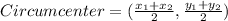
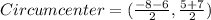
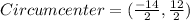
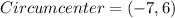
Therefore, the circumcenter of the triangle ABC is (-7,6).