Question

Suppose the life of a particular brand of laptop battery is normally distributed with a mean of 8 hours and a standard deviation of 0.6 hours. What is the probability that the battery will last more than 9 hours before running out of power?

0.4525
0.9525
1.6667
0.0478

Answer 1

Answer: 0.0478

Explanation:

Given : The life of a particular brand of laptop battery is normally distributed with a mean of 8 hours and a standard deviation of 0.6 hours.

i.e.
`\mu=8`

`\sigma=0.6`

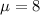
Let x be the random variable that represents the life of a particular brand of laptop battery.

Then , the probability that the battery will last more than 9 hours before running out of power will be :-

`P(x>9)=P(z>(9-8)/(0.6))` [∵
`z=(x-\mu)/(\sigma)`]

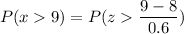`=P(z>1.6667)=1-P(z\leq1.6667)` [∵ P(Z>z)=1-P(Z≤z)]

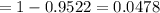`=1-0.9522=0.0478` [using P-value table for z]

Hence, the probability that the battery will last more than 9 hours before running out of power = 0.0478