Answer:
Twelve-fifths.
Explanation:
The diagram is shown below
Given triangle be right angled at
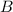 ,
,
Withe reference to
 ,
,
Its opposite side is
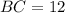 , adjacent side is
, adjacent side is
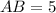 and hypotenuse is
and hypotenuse is
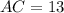
We are to find the value of
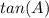
We know
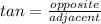
Substituting the above values we get,
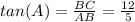
So the answer is Twelve-fifths.