Question

Given P(12,-2), Q(5,-10), R(-4,10) and S(4,y), find the value of y so that line PQ is perpendicular to line RS

Answer 1

The value of y is 3.

Explanation:

Given points: P(12,-2), Q(5,-10), R(-4,10) and S(4,y).

We need to find the value of y so that line PQ is perpendicular to line RS.

Slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

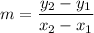
Slope of PQ is

`m_(PQ)=(-10-(-2))/(5-12)=(-8)/(-7)=(8)/(7)`

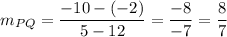
Slope of RS is

`m_(RS)=(y-10)/(4-(-4))=(y-10)/(8)`

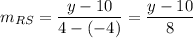
The product of slopes of two perpendicular lines is -1.

`m_(PQ)* m_(RS)=-1`

`(8)/(7)* (y-10)/(8)=-1`

`(y-10)/(7)=-1`

`y-10=-7`

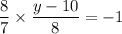
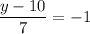
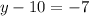
Add 10 on both sides.

`y=-7+10`

`y=3`

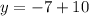
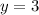
Therefore, the value of y is 3.