Question

A 1.80-kg object is attached to a spring and placed on frictionless, horizontal surface. A horizontal force of 17.0 N is required to hold the object at rest when it is pulled 0.200 m from its equilibrium position (the origin of the x axis). The object is now released from rest from this stretched position, and it subsequently undergoes simple harmonic oscillations.

(a) Find the force constant of the spring.N/m(b) Find the frequency of the oscillations.Hz(c) Find the maximum speed of the object.m/s(d) Where does this maximum speed occur?x =

Answer 1

Step-by-step explanation:

It is given that,

Mass of the object, m = 1.8 kg

Horizontal force acting on the object, F = 17 N

The object is pulled 0.2 meters from its equilibrium position. It is the amplitude of oscillation.

(a) We know from the Hooke's law that the force in simple harmonic motion is given by :

`F=kx`

`k=(F)/(x)`

`k=(17\ N)/(0.2\ m)`

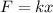
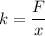
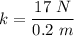
k = 85 N/m

(b) Let
`\omega` is the frequency of the oscillations. It is given by :

`\omega=\sqrt{(k)/(m)}`

`\omega=\sqrt{(85\ N/m)/(1.8\ kg)}`

`\omega=6.87\ rad/s`

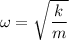
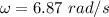
(c) Let v is the maximum speed of the object. In SHM, the maximum speed of the object is given by :

`v_(max)=\omega* A`

`v_(max)=6.87* 0.2`

`v_(max)=1.37\ m/s`

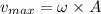
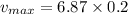
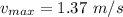
(d) At mean position, the speed of object is maximum. It means at x = 0, the speed of the object is maximum.

Hence, this is the required solution.