Answer:
The relation for the area of circle with radius , Diameter , circumference is
A=
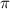 × radius²
× radius²
A =
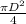
A =
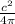
Explanation:
Given as :
The formula for the area of circle =
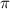 × radius²
× radius²
I.e A =
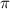 × radius²
× radius²
Now If we know radius then
Area calculated as A=
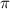 × radius²
× radius²
If we know Diameter then
Area calculated as
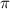 × (
× (
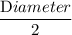 )²
)²
Or, A =
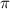 × (
× (
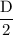 )²
)²
I,e A =
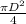
If we know the circumference then
∵ circumference = c = 2 ×
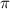 × radius
× radius
or, c = 2 ×
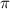 × r
× r
from here we calculate radius
I.e r =
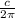
And So , Area ( A ) =
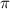 × radius²
× radius²
I.e A =
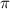 × (
× (
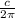 )²
)²
Or, A =
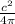
Hence The relation for the area of circle with radius , Diameter , circumference is
A=
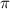 × radius²
× radius²
A =
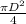
A =
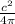 Answer
Answer