Question

Find the length of side x in the simplest radical form with a rational denominator

Answer 1

The value of x = 1

Explanation:

Given

• hypotenuse = √2

• angle Ф = 45°

To determine

x = ?

Using the trigonometric ratio

cos Ф = adjacent / hypotenuse

here

Ф = 45°

adjacent of 45° = x

hypotenuse = √2

so substituting Ф = 45° adjacent = x and hypotenuse = √2 in the equation

cos Ф = adjacent / hypotenuse

`\cos \left(45^(\circ \:)\right)=(x)/(√(2))`

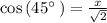
switch sides

`(x)/(√(2))=\cos \left(45^(\circ \:)\right)`

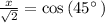
Multiply both sides by 2

`(2x)/(√(2))=2\cos \left(45^(\circ \:)\right)`

`√(2)x=√(2)` ∵
`\cos \left(45^(\circ \:)\right)=(√(2))/(2)`

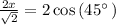
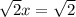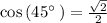
Divide both sides by √2

`(√(2)x)/(√(2))=(√(2))/(√(2))`

`x=1`

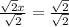
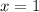
Therefore, the value of x = 1