Question

A horizontal circular wire loop of radius 0.7 m lies in a plane perpendicular to a uniform magnetic field that is pointing down from above into the plane of the loop, and has a constant magnitude of 0.44 T. If in 0.14 s the wire is reshaped from a circle into a square, but remains in the same plane, what is the magnitude of the average induced?

Answer 1

`\epsilon=1.10\ V`

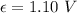
Step-by-step explanation:

It is given that,

Radius of the circular loop, r = 0.7 m

Magnetic field, B = 0.44 T

In 0.14 s the wire is reshaped from a circle into a square, but remains in the same plane.

Area of the circular wire,

`A_1=\pi r^2`

`A_1=\pi (0.7)^2=1.539\ m^2`

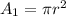
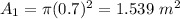
For the area of square,

The circumference of wire,
`C=2\pi r=2\pi * 0.7=4.39\ m`

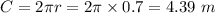
Side of square,
`l=(4.39)/(4)=1.09\ m`

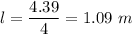
Area of square,
`A_2=1.09^2=1.188\ m^2`

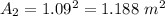
An emf is induced in the loop due to change in its area. The induced emf is given by :

`\epsilon=-B(dA)/(dt)`

`\epsilon=-B(A_2-A_1)/(t)`

`\epsilon=-0.44* (1.188-1.539)/(0.14)`

`\epsilon=1.10\ V`

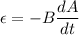
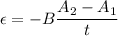
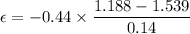
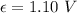
So, the magnitude of the average induced emf is 1.10 volts. Hence, this is the required solution.