Question

What is the answer to this solution. -7r−4≥ 4r+2

Answer 1

The solution is:

`-7r-4\ge \:\:4r+2\quad \::\quad \:\begin{bmatrix}\mathrm{Solution:}\:&\:r\le \:\:-(6)/(11)\:\\ \:\:\mathrm{Decimal:}&\:r\le \:\:-0.54545\dots \:\\ \:\:\mathrm{Interval\:Notation:}&\:(-\infty \:\:,\:-(6)/(11)]\end{bmatrix}`

Please check the attached line graph below.

Explanation:

Given the expression

`-7r-4\ge \:4r+2`

Add 4 to both sides

`-7r-4+4\ge \:4r+2+4`

Simplify

`-7r\ge \:4r+6`

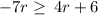
Subtract 4r from both sides

`-7r-4r\ge \:4r+6-4r`

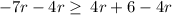
Simplify

`-11r\ge \:6`

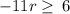
Multiply both sides by -1 (reverses the inequality)

`\left(-11r\right)\left(-1\right)\le \:6\left(-1\right)`

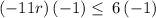
Simplify

`11r\le \:-6`

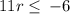
Divide both sides by 11

`(11r)/(11)\le (-6)/(11)`

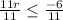
Simplify

`r\le \:-(6)/(11)`

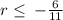
Therefore, the solution is:

`-7r-4\ge \:\:4r+2\quad \::\quad \:\begin{bmatrix}\mathrm{Solution:}\:&\:r\le \:\:-(6)/(11)\:\\ \:\:\mathrm{Decimal:}&\:r\le \:\:-0.54545\dots \:\\ \:\:\mathrm{Interval\:Notation:}&\:(-\infty \:\:,\:-(6)/(11)]\end{bmatrix}`

Please check the attached line graph below.