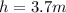Question

In a show, a 75.0-kg man swings from a 10.8m-long rope that is initially horizontal. At the lowest point of the swing, he picks up a 51.5-kg woman in a perfectly inelastic collision. Ignoring any frictional forces, how high would they reach in their upward swing?

Answer 1

`h=3.7 m`

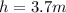
Step-by-step explanation:

Apply the theorem of the work and conservation of energy the motion have two steps the first without picks up the woman

`W_g=K_f-K_i`

`K_i=0`

`K_f=(1)/(2)*m_1*v_1^2=(1)/(2)75kg*v_1^2`

`W_g=m*g*R`

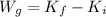
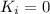
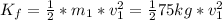
Solve to v'

`m*g*R=(1)/(2)*m*v^2`

`v^2=2*g*R`

`v=√(2*9.8m/s^2*10.8m)=√(211.68m^2/s^2)`

`v=14.54 m/s`

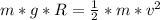
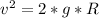
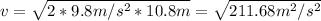
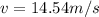
The momentum is conserved so the momentum as a perfectly inelastic collision give that the woman began in rest so

`p_1-p_2=pf`

`m*v_1+m_2*v_2=(m_1+m_2)v_t`

`v_2=0`

`75.0kg*14.5 m/s=(75.0kg+51.5kg)*v_t`

`v_t=(1091 kg*m/s)/(75.0kg+51.5kg)=8.6m/s`

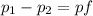
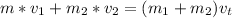
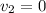
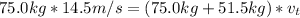
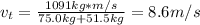
Finally the kinetic energy is the same of the potential energy so can find the high the reach in their upward swing

`K_t=E_p`

`(1)/(2)*(m_1+m_2)*v_t^2=(m_1+m_2)*g*h`

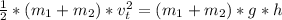
Solve to h'

`h=(v_t^2)/(2*g)=((8.6m/s)^2)/(2*9.8m/s^2)=(73.96 m^2/s^2)/(19.6m/s^2)`

`h=3.7 m`