Question

How many zero pairs must be added to the function

f(x) = x - 10x - 4 in order to begin writing the function in

vertex form?

4

10

21

25

Answer 1

Option 4 - 25

Explanation:

Given : Function
`f(x)=x^2-10x-4`

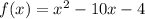
To find : How many zero pairs must be added to the function in order to begin writing the function in vertex form?

Solution :

The vertex form is
`y=(x-h)^2+k`

Let function
`y=x^2-10x-4`

Applying completing the square,

Add and subtract square of half of the coefficient of x,

i.e.
`((-10)/(2))^2=(5)^2`

`y=x^2-10x-4+(5)^2-(5)^2`

`y=x^2-2* 5* x+(5)^2-4-25`

`y=(x-5)^2-29`

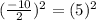
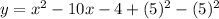
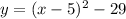
Therefore, the zero pairs must be added to the function in order to begin writing the function in vertex form is 25.

So, Option 4 is correct.