Question

You have an evacuated, iron spherical shell and want to know how thick the shell wall is. However, you cannot cut open the iron shell to measure the thickness of the wall. The ball just floats once completely submerged in water, and you measure the outer diameter to be 58.7 cm. If the density of iron is 7.87 g/cm3, what is the thickness of the wall?

Answer 1

26 cm

Step-by-step explanation:

V = Volume

R = Outer radius of the shell = 58.7 cm

r = Inner radius of the shell

g = Acceleration due to gravity = 9.81 m/s²

\rho = Density

As the shell is completely submerged

Force on shell

`F=v\rho g\\\Rightarrow F=(4)/(3)\pi R^3* 1000g`

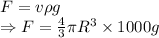
Weight of the shell

`W=(4)/(3)\pi (R^3-r^3)* 7870g`

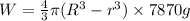
Equating the two equations as the forces are conserved

`(4)/(3)\pi R^3* 1000g=(4)/(3)\pi (R^3-r^3)* 7870g\\\Rightarrow R^3* 1000=(R^3-r^3)* 7870\\\Rightarrow R^3=(R^3-r^3)(7870)/(1000)\\\Rightarrow R^3=(R^3-r^3)7.87\\\Rightarrow 6.87R^3=r^37.87\\\Rightarrow r=\left((6.87)/(7.87)*0.587^3\right )^{(1)/(3)}\\\Rightarrow r=0.561\ m`

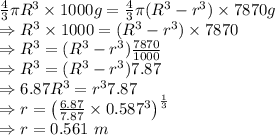
Inner radius of the shell is 0.561 m

The thickness of the wall is 0.587-0.561 = 0.026 m = 26 cm