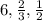Question

If f(x) = 6x^3 - 29x^2 -40x -12 and f(6) = 0, then find all the zeros of f(x) algebraically

Answer 1

`6, (2)/(3),(1)/(2)`

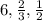
Explanation:

Since 6 is a zero f f(x), then (x-6) is a factor of f(x). Now we will find the others factors

First, we divide f(x) by x-6:

1. divide the highest degree coefficients of the denominator
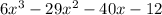`6x^3-29x^2-40x-12` and divisor
`x-6`:

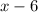quotient:
`(6x^3)/(x)=6x^2`

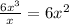
2. Multiply
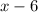`x-6` by
`6x ^ 2`:
`6x^3-36x^2`.

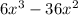Subtract
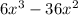`6x^3-36x^2` from
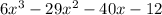`6x^3-29x^2-40x-12` to obtain a new remainder:
`7x^2-40x-12`

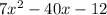
Now, divide the new remainder by
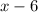`x-6`. We repeat the previous steps:

3. quotient:
`(7x^2)/(x)=7x`

4. Multiply
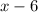`x-6` by
`7x`:
`7x^2+42x`

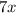Subtract
`7x^2+42x` from
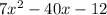`7x^2-40x-12` to obtain a new remainder:
`2x-12`.

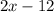5. Divide
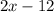`2x-12` by
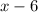`x-6`. We obtain
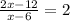`(2x-12)/(x-6)=2` and the new remainder is 0.

So, the quotiente
`(6x^3-29x^2-40x-12)/(x-6)=6x^2+7x+2`

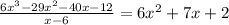
Then,
`6x^3-29x^2-40x-12=(x-6)(6x^2+7x+2)`

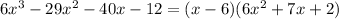
For find the other two zeros of f(x) we have the zeros of
`6x^2+7x+2`.

We use the formula:
`x_(1,2)=(-b\pm√(b^2-4ac))/(2a)`,

Then,
`x_(1,2)=(7\pm√(7^2-4*6*2))/(2*6)=(7\pm 1)/(12)\\x_1=(8)/(12)=(2)/(3)\\x_2=(6)/(12)=(1)/(2)`

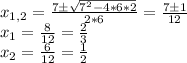
Then the zeros of f(x) are:
`6, (2)/(3),(1)/(2)`