Answer:
Perimeter of triangle = 12 + 9 + 15
= 36 units
Therefore, option A is correct.
Explanation:
The given points
From the table, it is clear the side containing the line segment joining the points (-4, 5) and (8, 5) is a straight horizontal line.
Thus, the length of the horizontal distance from the points (-4, 5) and (8, 5) will be:
8-(-4) = 12 units
From the table, it is clear the side containing the line segment joining the points (8, 5) and (8, -4) is a straight vertical line.
Thus, the length of the vertical distance from the points (8, -4) and (8, 5) will be:
5-(-4) = 9
Now, finding the length of the side containing the segment (8, -4) and (-4, 5) using the formula:
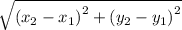
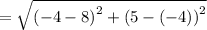
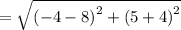
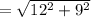
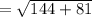
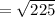
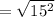
![\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a^n}=a](https://img.qammunity.org/2022/formulas/mathematics/college/e2b9759asiw9imonzdathjm9nljkz8ke1s.png)
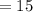
We know that the Perimeter of a rectangle is the length of all the sides of the triangle. Therefore, combining all the lengths of the line segments
Thus,
Perimeter of triangle = 12 + 9 + 15
= 36 units
Therefore, option A is correct.