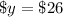Question

Jane’s buying clothes. She can get 5 shirts & 4 sweaters for $229 or she can get 2 shirts & 3 sweaters for $128. How much is 1 shirt, and how much is 1 sweater?

Answer 1

Cost of 1 shirt is
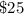`\$25` and cost of one sweater is
`\$26`

Solution:

Given that Jane’s buying clothes.

She can get 5 shirts & 4 sweaters for
`\$229`

She can get 2 shirts & 3 sweaters for
`\$128`

Need to determine cost of 1 shirt and 1 sweater.

Let assume cost of 1 shirt =
`\$x`

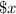
And assume cost of 1 sweater =
`\$y`

Let us create equations from give conditions

First condition is Cost of 5 shirt + cost of 4 sweater =
`\$229`

`\begin{array}{l}{\text { cost of 5 shirts }=5 * \text { cost of 1 shirt }=5 * x=5 x} \\\\ {\text { cost of 4 sweater }=4 * \text { cost of 1 sweater }=4 * y=4 y}\end{array}`

So using first condition equation which we get is as follows

`5 x+4 y=229 \rightarrow (1)`

Second condition is Cost of 5 shirt + cost of 4 sweater =
`\$128`

`\begin{array}{c}{\text { cost of } 2 \text { shirts }=2 * \text { cost of } 1 \text { shirt }=2 * x=2 x} \\\\ {\text { cost of } 3 \text { sweater }=3 * \text { cost of } 1 \text { sweater }=3 * y=3 y}\end{array}`

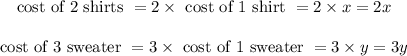
So using second condition equation which we get is as follows

`2 \mathrm{x}+3 \mathrm{y}=128\quad\rightarrow (2)`

Now we have two equations to be solved

`\begin{array}{l}{5 x+4 y=229 \rightarrow (1)} \\\\ {2 x+3 y=128 \rightarrow (2)}\end{array}`

On multiplying equation (1) by 2 and equation (2) by 5 to make coefficients of x equal in both equations, we get

`\begin{array}{l}{2 x(5 x+4 y)=2* 229} \\\\ {10 x+8 y=458 \rightarrow (3)} \\\\ {5 x(2 x+3 y)=5 * 128} \\\\ {10 x+15 y=640 \rightarrow (4)}\end{array}`

On subtracting (3) from (4), we get

`\begin{array}{l}{(10 \mathrm{x}-10 \mathrm{x})+(15 \mathrm{y}-8 \mathrm{y})=640-458} \\\\ {\Rightarrow 7 \mathrm{y}=182} \\\\ {\Rightarrow \mathrm{y}=(182)/(7)=26}\end{array}`

On substituting y = 26 in equation (1) we get

`\begin{array}{l}{\Rightarrow 5 \mathrm{x}+(4 * 26)=229} \\\\ {\Rightarrow 5 \mathrm{x}=229-104} \\\\ {\Rightarrow 5 \mathrm{x}=125} \\\\ {\Rightarrow \mathrm{x}=(125)/(5)=25}\end{array}`

Cost of 1 shirt =
`\$x = \$25`

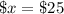
Cost of 1 sweater =
`\$y = \$26`