Answer:
The probability that X is less than 32 minutes is 0.736.
Explanation:
Given : The random variable X is exponentially distributed, where X represents the time it takes for a person to choose a birthday gift. If X has an average value of 24 minutes.
To find : What is the probability that X is less than 32 minutes?
Solution :
If X has an average value of 24 minutes.
i.e.
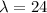
The random variable X is exponentially distributed, where X represents the time it takes for a person to choose a birthday gift.
The exponentially function is
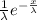
The function form according to question is
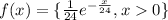
The probability that X is less than 32 minutes is
![P[x<32]=1-e^{-(32)/(24)}](https://img.qammunity.org/2020/formulas/mathematics/college/1o5l388p9tsljp6hzi48bt0wufp12tdx0k.png)
![P[x<32]=1-0.26359](https://img.qammunity.org/2020/formulas/mathematics/college/m7cnis1pj8an5lvm7a4s8i7cxlp7n7rxb0.png)
![P[x<32]=0.736](https://img.qammunity.org/2020/formulas/mathematics/college/sykcj6odb6oxj9sfjktdl2n3z4f9n0b9h6.png)
Therefore, the probability that X is less than 32 minutes is 0.736.