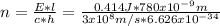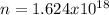Answer:
Photons strike the CD
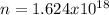
Step-by-step explanation:
First of all, it is necessary to calculate the energy produced by a semiconductor laser for 69 minutes:
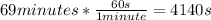

Next, it is possible to calculate the number of photons striking the CD surface during this time:
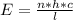
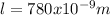 long in CD
long in CD
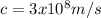 light velocity
light velocity
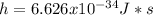
Solve to n'