In parallelogram ABCD, AD = 12 in, m∠C = 46º, m∠DBA = 72º. Find the area of ABCD.

Question

asked Nov 25, 2020 74.3k views

2 Answers

Mukil Deepthi · Answer 1 · 2020-12-01T17:42:37+0000

Answer:

96.16 square in

Explanation:

Given information: In parallelogram ABCD, AD = 12 in, m∠C = 46º, m∠DBA = 72º.

Opposite angles of a parallelogram are congruent.

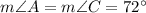
$m\angle A=m\angle C=72^(\circ)$

According to the angle sum property, the sum of interior angles of a triangle is 180º.

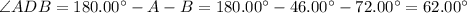
$\angle ADB=180.00^(\circ)-A-B=180.00^(\circ)-46.00^(\circ)-72.00^(\circ)=62.00^(\circ)$

Law of Sine:

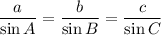
$(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)$

Using Law of Sine we get

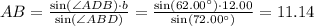
$AB=(\sin(\angle ADB)\cdot b)/(\sin(\angle ABD))=(\sin(62.00^(\circ))\cdot 12.00)/(\sin(72.00^(\circ)))=11.14$

It means the base of parallelogram is 11.14 in.

Draw an altitude on AB from D.

In a right angle

$\sin \theta = (opposite)/(hypotenuse)$

In triangle ADE,

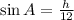
$\sin A= (h)/(12)$

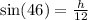
$\sin (46)= (h)/(12)$

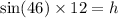
$\sin (46)* 12=h$

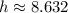
$h\approx 8.632$

The height of the parallelogram is 8.632.

The area of parallelogram is

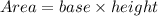
Area=base* height

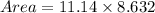
Area=11.14* 8.632

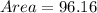
Area=96.16

Therefore, the area of parallelogram is 96.16 square in.