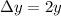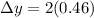Question

A lecturer is demonstrating two-slit interference with sound waves. Two speakers are used, 1.9 m apart. The sound frequency is 1220 Hz and the speed of sound is 343 m/s. Students sit facing the speakers in a row of seats 6.2 m away. Along the row of students, what is the spacing between the locations on either side of the center line between the speakers where no sound is heard because of destructive interference? The angle may be to large to use small angle approximation. Answer in units of m.

Answer 1

`\Delta y = 0.92 m`

Step-by-step explanation:

As we know that the speed of the sound in air is

`v = 343 m/s`

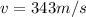
frequency of the sound is

`f = 1220 Hz`

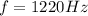
now the wavelength is given as

`\lambda = (v)/(f)`

`\lambda = (343)/(1220)`

`\lambda = 0.28 m`

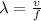
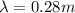
now the position of minimum is given as

`d sin\theta = (\lambda)/(2)`

`1.9 sin\theta = (0.28)/(2)`

`\theta = 4.24 degree`

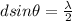
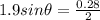
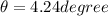
now the position of minimum intensity is given as

`y = L tan\theta`

`y = 6.2 tan4.24`

`y = 0.46 m`

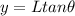
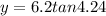
so the separation between the minimum intensity on either sides is given as

`\Delta y = 2y`

`\Delta y = 2(0.46)`

`\Delta y = 0.92 m`