Question

A top-loading washing machine has a cylindrical basket that rotates about a vertical axis. The basket of one such machine starts from rest and reaches an angular speed of 4.0 rev/s in 9.0 s. The lid of the machine is then opened, which turns off the machine, and the basket slows to rest in 13.0 s. Through how many revolutions does the basket turn during this 22 s interval? Assume constant angular acceleration while it is starting and stopping.

Answer 1

`n_(tot)=44rev`

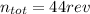
Explanation:

In order to solve this problem we can make use of the following formula:

`\theta=((\omega_(f)+\omega_(0))/(2))t`

where θ is the total angle the basket has turned, ω is the angular velocity and t is the time.

Generally theta is written in radians and omega is written in radians per second. Now, since the revolutions are directly related to the radians and they want us to write our answer in revolutions, we can directly use the provided speeds in the formula, so we can rewrite it as:

`n=((f_(f)+f_(0))/(2))t`

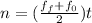
where n represents the number of revolutions and f is the frequency at which the basket is turning.

The movement of the cylindrial basket can be split in two stages, when it accelerates and when it decelerates. So let's analye the first stage:

`n=((4rev/s+0)/(2))(9s)=18rev`

and now let's analyze the second stage, where it decelerates, so we get:

`n=((0rev/s+4rev/s)/(2))(13s)=26rev`

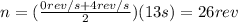
So now that we know how many revolutions the cylindrical basket will take as it accelerates and as it decelerates we can add them to get:

n=18rev+26rev=44rev

So the basket will turn a total of 44 revolutions during this 22s interval.